https://www.omegastatistics.com/wp-content/uploads/2022/05/Whitepaper-Which-Statistical-Test.pdf
Omega Statistics Blog
Normalization and Standardization
The nice thing about being delayed for 3 hours at the airport is that it gives you time to catch up on reading and to write blog posts. And the airline feeds you snacks. And you can share the snacks with the little bird who is flying around inside the terminal. My new sparrow friend, I call him Peanut, liked the crust of my PBJ and also seems to enjoy Cheetos (the crunchy ones, not the puffs).
So, before I give tiny Peanut (or not so tiny Me) diabetes, I think this is a good time to put away the little bag of cookies and discuss two things we can do to our variables prior to analysis, normalization and standardization.
Why would we do this to our data? Because sometimes we want to compare data measured in different units, to more accurately or easily see the differences. We normalize or standardize to take away the units of measure and just look at the magnitude of the measurements on one uniform scale. Normalization and standardization allow us to take apples and oranges and compare them like they are both the same fruit.
Mathematically, normalization and standardization are needed when measurements are being compared via Euclidean distance. I’ll let you research the math stuff on your own.
An example for using normalization or standardization would be comparing test scores on two different tests, say, an English test that has a range of scores from 50 to 250 and a math test that has a range of scores from 200 to 400. If we were to leave the scores as is and compare students’ scores on each test to see which test they performed better on, then of course almost everyone would do better at math.
And we know not everyone does better at math! So, we need to scale the scores in a way that will allow us to compare the scores on an even playing field.
Normalization
You will see the word normalization used for many different approaches to data transformation. In this post, I am describing the normalization technique of “feature scaling” which is used to make all of the raw data values fit into a range between 0 and 1.
And since statisticians have at least three names for everything, it is also called “min-max” normalization and “unity” normalization.
To normalize a variable to a range between 0 and 1 you need the lowest value and the highest value of the measurements on the variable and then use a simple formula to use on each measurement:
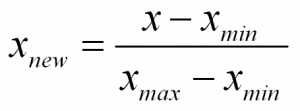
In words:
Normalized Measurement = (original measurement – minimum measurement value) divided by (maximum measurement value – minimum measurement value)
There numerous techniques for normalizing variables. A few are normalizing within a range of (-1 to 1), and mean normalization. And you might want to check out the coefficient of variation too.
Standardization
Standardization is a type of feature scaling and you may even hear it referred to as normalization. The formula below will transform your data so that the mean will be 0 and the standard deviation will be 1 (called a unit standard deviation).
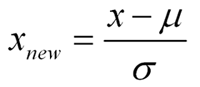
In words:
Standardized Measurement = (original measurement – mean of the variable) divided by (standard deviation of the variable)
When to Normalize? When to Standardize?
In many cases you can use normalization or standardization to scale your variables. However, if you have many outliers, normalization will not show outliers as well, because all data is scaled between two numbers (0,1).
On the other hand, standardization does not have any constraint on the resulting range of numbers. So, although in a normal distribution we would like the range of numbers to be between -3 and 3, they don’t have to be…so you will see outliers (such as values of say, -5 or 3.4, etc.) more easily.
Also, standardization makes it easy to see if a particular measurement is above or below the mean because negative numbers will be below the mean of 0 and positive numbers will be above the mean of 0.
And retaining the spread using standardization allows one to assign probabilities to measurements, and percentiles, while taking into account the spread of the data
References:
https://www.statisticshowto.datasciencecentral.com/normalized/
Meta-Analysis and the Rewards of Persistence

Let’s say you would like to estimate the efficacy of a treatment or intervention but you don’t have the time, money, or other resources to design and implement an actual study. However, there are studies that have been performed by others. These studies can be reviewed and mined for information that will help you to investigate treatment effects. This is where a meta-analysis comes in handy.
In essence, a meta-analysis is an analysis of analyses. You can take the information obtained from a systematic review of the literature and obtain a pooled effect size and associated confidence interval for the treatment of interest.
Recently I worked on a rather large systematic review and meta-analysis of articles for a study on a therapeutic intervention for patients with dementia. The studies included a treatment group (sometimes more than one treatment group), and a control group, as well as baseline measurements, and one or more follow-up measurement times.
The outcomes of interest included continuous level measurements obtained from many different scales and survey instruments. Some scales/instruments were scored so that higher scores indicated improvement in functioning, whiles others were scored so that lower scores indicated improvement.
Deriving a pooled effect of treatment when there are numerous variations on measurement times, outcomes, and directions of the effects can be difficult. I needed to use special techniques to derive effect sizes and standard errors for each individual study and outcome. I ended up using standardized mean differences (SMD) which I could obtain from F-statistics, eta-squared values, or, if I was lucky, and the information was available, from the means and standard deviations for each group (treatment vs. control) at baseline and at the end of each study.
Oh, and many times, a single study would have numerous outcomes. What fun!
You’d think that computing the effect sizes for a conglomeration of studies with various designs, methods, and measurements would be the hard part…it wasn’t too bad once I figured it out. Here are some references and resources I used for computing the effects:
The hard part was finding a way to compile the effect sizes into the pooled effect AND to design pretty forest plots that showed both (a) the individual studies and (b) the individual tests (outcomes) that were nested inside of each study.
Many online resources and effect size calculators involved computing odds ratios from count data. But I had SMD’s from continuous data. Bummer…
There are some very nice meta-analysis functions in Stata but I really struggled with getting the forest-plots to look pretty. I MUST HAVE PRETTY! And preferably without too much coding, gnashing of teeth and hair-pulling.
There is a software, Comprehensive Meta-Analysis (CMA), which offers a free trial. And I tried the trial and it is very comprehensive! But again, I couldn’t get the forest plots to look the way I wanted them to look
Finally, I came across an Excel add-on called MetaEasy, by Evangelos Kontopantelis and David Reeves.
Excel? Really? Oh yes. And it was awesome. And FREE, my favorite four-letter word. The add-on was easy to install, the instructions were easy to follow. And the forest plots were very pretty.
Here is a link which includes the download for MetaEasy, an instruction manual, and an Excel spreadsheet with example data.
Here is a link to an example Excel spreadsheet I made using MetaEasy. In honor of the great Stan Lee I decided to compile it with studies of 11 of Mr. Lee’s superheroes with outcomes of improvement in mental health conditions based on the article, “10 Mental Health Problems Superheroes Suffer” I just made this up for demonstration purposes kiddos. So I don’t wish to discuss the details of who has what or why. Just have fun with it.
I often find that if I keep digging I will hit treasure (not always, sometimes I puncture a sprinkler line). And I am happy to share this lovely golden nugget with you. Enjoy!
Unique Identifiers. Gotta Have ‘Em!

Before you use your data set you must be sure that each record in your data has a unique identifier (unique ID).
Why? The best reason to assign unique ID’s is for tracking purposes. Trust me, you will run into a situation where a need to backtrack is necessary. There are many reasons, but here are two:
A unique identifier (ID) can be anything, as long as each record in your data set has a unique one of this thing. Typically a unique identifier is numeric, but it doesn’t have to be. If your data consists of survey respondents, you could use each respondents email (assuming respondents haven’t shared an email address!). Or maybe you’d like to use alpha-numeric ID’s. A way to determine what would work for your data is to ask, “What is the best unique information I have about the records in my data set?” You can then think about ways to fashion a nice unique ID for each record.
Ok, you aren’t sure how to fashion your unique ID numbers for your records, or maybe you don’t really care about specifics of the unique ID, just that each record has one. Here are some tips on creating unique ID’s using SPSS software. I hope you find them useful!
Let’s assume that your data is in a typical structure of a typical data set and you want to make a variable (a column) that gives each record (row) a unique identification number (ID).
Here is some SPSS syntax to use to give a unique ID to each record in the dataset. The unique ID number will be the same as the row number of the record. SPSS refers to the row number as the “case number”.
COMPUTE ID = $casenum.
FORMAT ID (F8.0).
EXECUTE.
The FORMAT command says to give the variable you are creating (ID) for your unique ID number 8 digits, and 0 decimal places. ID’s don’t really need decimal places, but if you want to, just change the 0 to whatever number you want.
Ok, easy peasy! But, what if you have a dataset in long format, with repeated measurements for some folks?
I recently worked on a data set that included 3 years of data, but some participants were only in 1 year, some were in 2 years, and some others were in all 3 years.
Every person had their own unique ID number, but the numbers were very long and it was hard to see the matches. And, I wanted to also see how many participants were in only 1 year, 2 years, or 3 years respectively.
Another time you may want to do this is when you want to protect confidentiality of the participants. If the ID’s are traceable to participant records, such as patient numbers in hospital records or students in school records, or hey, the participant names are in the dataset! Then a new number that can’t be used to match to those records to outside sources should be created.
So I needed to have unique ID numbers to replace the current ID numbers, and also needed to include a coding sequence for the possibility of a person having more than one measurement time. And, I wanted to know how many people were represented once, twice, or three times.
I used these steps:
1. First sort cases by the name or ID of the individuals.
SORT CASES BY current_id(A).
2. Under the “Data” pull down menu, choose “Identify Duplicate Cases”.
— Define matching cases by: Move over the variable that is currently the ID into the box.
— In the “Variables to Create” box, check the “Indicator of primary cases” box and specify “First Case in Each Group is primary” You will see a variable name such as “PrimaryFirst” in the box to the right. You can change the name to whatever you want.
But I usually leave it as is.
— Also check the box by “Sequential count of matching” this will count the number of instances each participant is represented.
— Uncheck the “Move Matching cases to the top of the file” box. I don’t want to move anything around just yet.
— But do check the “Display frequencies for created variables” box.
3. Click “OK”.
4. You should now have two variables at the right of the data set (a) PrimaryFirst and (b) MatchSequence. And you will have some output with frequencies of the matches etc.
5. Now, we will use the two variables we created and some syntax to give the unique ID’s and they will be based on the case number variable. This syntax will give unique ID’s.
BUT you will have some gaps in the numbering sequence due to the use of the case numbers to define the ID’s. For instance, you most likely won’t have ID that run 1, 2, 3, 4, 5, …. But they will be 1, 3, 4, 6, etc. Still UNIQUE though, and that is what we want!
Here is the syntax to run:
DO IF (PrimaryFirst EQ 1).
COMPUTE ID = $casenum.
else.
COMPUTE ID = lag(ID).
end if.
EXECUTE.
There should now be a variable called “ID” with a unique number given to each participant. You can now make a back-up of the file and don’t touch this one any more. Save the file also as a working file and then delete the “traceable” identifiers you don’t want to use from you working file.
This working file will be used for all analyses, and sent to whomever needs to see it, but now you have, hopefully, protected some confidentiality of records.
Also, you can use your new ID variable, and the MatchSequence variable as an index variable, if you need to transpose your data from long to wide.
Now you’ll know who’s who and what’s what! 🙂
Independent Samples t-test in Excel for Summary Data

I recently had to run a series of independent samples t-tests on summary data, meaning I only had the group means, standard deviations, and sample sizes. There are online calculators available to do the job.
But my client needed more information on what was going on behind the scenes of the calculations, and I needed a record of what I did. I looked for a way to run summary t-tests in SPSS and even R, and I couldn’t find a way.
So I did what any gal with some stats knowledge and some coding experience would do.
I made this calculator in Excel.
Thanks to Todd Grande for the inspiration. I built my calculator based on his criteria. His video will walk you through it if you’d like to build one of your own. Or, you can just watch his video to see how it works. Enjoy!
Control or Covariate?

As is the case with many statistical concepts, one can find many terms for the same idea. And for many studies covariates and controls do the same work, but we call them different names according to how we use the variable.
Technically, a covariate is a variable that is of no direct interest to the researcher, but one that may have an affect on the outcome (the dependent variable). Results of a study can be made more accurate by controlling for the variation in the covariate. So, a covariate is in fact, a type of control variable.
Examples of a covariate may be the temperature in a room on a given day of an experiment or the BMI of an individual at the beginning of a weight loss program. Covariates are continuous variables and measured at a ratio or interval level.
Technically, a control variable is a variable that is of no direct interest to the researcher….ok, it is more or less the same as a covariate, except, a control variable does not co-vary from record to record.
This is the difference between covariates and controls in a study. For example, a covariate such as BMI can be different for each individual in the study, and it is theoretically able to have an infinite number of values depending on how many decimal places you want to count.
A control variable is a nominal variable (not continuous) and although it has more than one value, the values are categorical and not infinite. Examples of a control variable could be the actual room number in which an experiment was conducted, or if an individual was underweight, normal weight, overweight, or obese.
Recently, a client needed to include a measure of socio-economic status (SES) in her study and decided to use the variable of income. She wanted to know if she should define income as a covariate or a control in her analysis of variance (ANOVA). Of course I told her, as many statisticians do, that “It depends.”
“On what?” you ask (and so did she). If we measure income in dollar amounts for each study participant, then we could use the information as a covariate, which would in turn make the ANOVA an analysis of co-variance (ANCOVA).
However, if the variable was measured according to income group, such as $0 to $25,000; $25,001 to $50,000; $50,001 to $75,000; etc. then the variable would be a control variable and entered into the ANOVA as another independent grouped variable.
So, both covariates and control variables can be considered “control variables”. The main difference is in the measurement level. If the variable is continuous, use it as a covariate. If you have categories, then you have an independent control variable. But don’t be surprised if you hear someone refer to a categorical control variable as a “covariate”. it is just the way of things in the wacky world of statistics.
Propensity Scores vs. Regression Adjustment for Observational Studies

Randomized controlled trials (RCTs) are considered the gold standard approach for estimating treatment effects. However, not all clinical research involves randomization of subjects into treatment and control groups. These studies are commonly referred to as non-experimental or observational studies. Some examples of non-experimental (observational) studies include:
In observational studies, the treatment selection is influenced by the characteristics of subjects. Therefore, any differences between groups are not randomized out, and the baseline characteristics of the subjects could differ between treatment and control groups. In essence, the baseline characteristics systematically differ and we must find a way to account for these systematic baseline differences.
Researchers often use regression adjustments to account for baseline differences between groups. A regression adjustment is made by using one or more (usually more) variables obtained at baseline as predictors, and one dependent variable of the treatment outcome. Using a regression adjustment to investigate baseline differences in observational studies has the following issues:
Propensity scores, and matching subjects from each of the study groups using propensity scores, are constructed without taking the treatment outcome into consideration. The use of propensity scores keeps the researcher’s attention on baseline characteristics only. However, once the subjects are scored and matched (defined as balanced), a regression model can be analyzed to further adjust for any residual imbalance between the groups. So regression models still have their use! But they are used after the propensity scoring and matching.
Propensity scores have the added benefit of allowing a researcher to see the actual amount of overlap, or lack of it, between treatment groups. After propensity scores are assigned to each individual in each group, then the researcher uses the scores to “match” pairs of subjects in the treatment with subjects in the control group. The easiest way to match is with a one-to-one match: one treatment subject to one control subject. But some, more-advanced matching techniques can match one-to-many.
After matching, the researcher can see if there are many unmatched individuals left over (indicative of large differences in baseline characteristics between the groups). A large difference between groups might not just indicate that the treatment and control groups differed at baseline, but that the differences between groups might be too large to assess any meaning on the outcome of the intervention. After all, the reason for propensity score matching is to derive groups that simulate equal baseline characteristics. If they can’t be matched, they were just not similar. Hence, treatment efficacy cannot be derived or established.
Here is a very simple example of the use of propensity scores and matching for a non-experimental study:
A study is performed to assess the treatment effects of two analgesic drugs given to patients presenting to an emergency room with severe cluster headaches. The type of drug given, A or B, is decided upon various factors such as the time span of the current headache, frequency of headaches, age of the patient, and various comorbidities. Thus, the patients were not randomized into the two drug treaments.
This non-randomization is also called “selection bias”. The clinician selected the treatment to give to each patient. If more than one clinician was involved in the decision making of treatment, we should control for this also! Perhaps some clinicians like one treatment over the other.
The outcome is time to pain management. And looking at the data without any adjustment, Drug A appears to relive pain significantly faster than Drug B. But, maybe this is not the case. Something else could be at work here, or maybe there isn’t a difference between the drugs at all. Or maybe the patients in Group A (patients who took drug A) are much too different from the patients in Group B (patients who took Drug B) to make any assessment of efficacy.
So, we will develop a propensity score for each patient based on the covariates we believe (or better, know from our knowledge and the literature). The propensity score, let’s call it Z, predicts how likely a person is to get Drug A.
We then group people with similar propensity scores between the two groups of patients, such that patients with, say, Z = .30 in Group A are matched with patients with Z = .30 in Group B.
Nothing is as good as the RCT, but I hope I’ve opened up your thinking a bit to the use of propensity scores in observational studies. There are many ways to score and match and analyze observational study groups. A good reference to start with is the article by Austin (2011) listed below. Rosenbaum and Rubin (1983) wrote the seminal work on propensity scores, but even I think it is a bit too theory heavy. But it is also listed in the references below if you are so inclined.
Not everyone likes propensity scores for matching cases. The article by King and Nielsen (2016, also referenced below) presents some limitations in propensity score matching and some remedies for when many individual cases remain after the matching attempt.
Stata has a function for tseffects for obtaining propensity scores, and the function of psmatch for propensity score matching. You can also run post-estimation regression with the functions.
For R fans, here is a nice tutorial on propensity score matching. Not as nice as the Stata code, but hey, it’s free! http://pareonline.net/pdf/v19n18.pdf
References
Austin, Peter. (2011). An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies. Multivariate behavioral research. 46. 399-424. 10.1080/00273171.2011.568786.
R. Rosenbaum, Paul & B Rubin, David. (1983). The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika. 70. 41-55. 10.2307/2335942.
Not everyone likes propensity scores for matching:
Gary King and Richard Nielsen. Working Paper. “Why Propensity Scores Should Not Be Used for Matching”. Copy at http://j.mp/2ovYGsW


